The place value of a digit in a number is the value it holds to be
at the place in the number. We know about the place value and face value
of a digit and we will learn about it in details.
We know
that each digit in a number has a place. The place that a digit occupies in a number
tells us about its place value.
Place Value of 3-Digit Numbers:
Each digit in a number has a place value depending on its place or position in the number.
For Example:
1. let us see the place value of 3 in 123, 231 and 312.

2. Let us take a 3-digit number 915
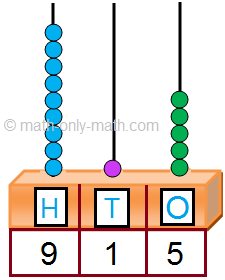 |
915 = 9 |
So, the place value of digit 9 is 9 hundred or 900.
The place value of digit 1 is 1 ten or 10.
The place value of digit 5 is 5 ones or 5.
Face Value of 3-Digit Numbers:
Face value of a digit is the same as the digit itself.
It does not depend on the place or position of the digit in a number.
The face value of 3 in each of the numbers 123, 231 and 312 is 3.
In fact, the face value of 3 will always be 3.
Place, Place Value and Face Value:
A number is formed by grouping the digits together.
● Each digit has a fixed position called its place.
● Each digit has a value depending on its place called the place value of the digit.
● The face value of a digit for any place in the given number is the value of the digit itself
● Place value of a digit = (face value of the digit) × (value of the place)
We know
that each digit in a number has a place value. The place a digit occupies in a
number tells us its place value. So, the product of the digit and the value of
the place it occupies gives us the place value. Let us arrange the digits of
the number 5,32,161 in the following place value chart.
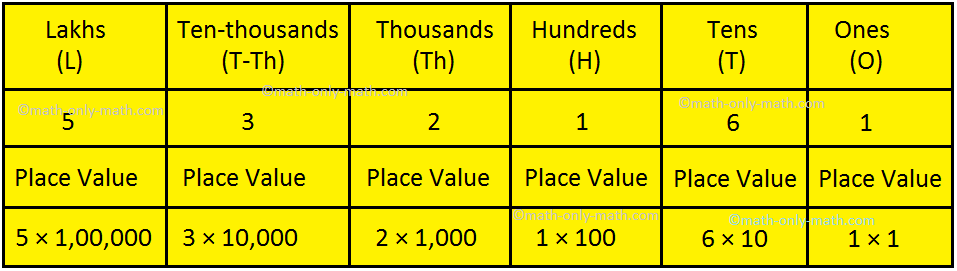
The face
value of a digit in a number is the digit itself.
Properties of Place Value:
1. The place value of every one-digit number is the same as and equal to its face value.
(i) Place value and face value of 1, 2, 3, 4, 5, 6, 7, 8 and 9 are 1, 2, 3, 4, 5, 6, 7, 8 and 9 respectively.
(ii) The place value of zero (0) is always 0. It may hold any place in a number, its value is always 0.
As, in 105, 350, 42017, 90218 the place value of 0 in each number is 0.
2. In a two-digit number, the place value of the ten-place digit is 10 times of the digit.
As, in 58, the place value of 5 is 5 × 10 = 50 and place value of 8 is 8 × 1= 8; the face value of 5 is 5 and of 8 is 8.
3. In the number 475, the digit 5 is at one’s place, digit 7 is at ten’s place and digit 4 is at hundred’s place.
So, place value of 5 = 5, place value of 7 = 7 × 10 = 70, and place value of 4 is 4 × 100 = 400.
Thus, for the place value of a digit, the digit is multiplied by the place value of 1 it has to be that place.
For Example:
In 768;
the place value of 8 = 8 × 1 = 8
the place value of 6 = 6 × 10 = 60 and
the place value of 7 is 7 × 100 = 700.
4. Now it is the general law that the digit possesses its place
value as the product of the digit and place value of one to be at that
position.
For Example:
(i) In a number 4129;
the place value of 9 is 9 × 1 = 9 as 9 is at one’s or unit’s place.
the place value of 2 is 2 × 10 = 20 as 2 is at ten’s place.
the place value of 1 is 1 × 100 = 100 as 1 is at hundred’s place.
the place value of 4 is 4 × 1000 = 4000 as 4 is at thousand’s place.
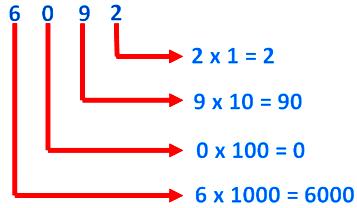
(ii) In a number 3720, the place value of
|
3 is 3 × 1000 = 3000 7 is 7 × 100 = 700 2 is 2 × 10 = 20 0 is 0 × 1 = 0 |
3 being at Th-place 7 being at H-place 2 being at T-place 0 being at one’s or unit’s place |
(iii) Place value of the digits 3702 are shown below:
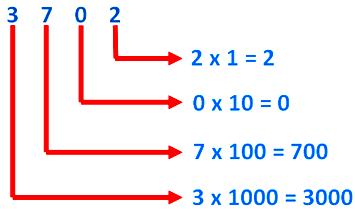
(iv) Here, we also see that the place value of the digit 0 in a number is always zero, whatever may be its position.
Place-value of a Digit in a Number:
We know that the position of a digit in a number determines
its corresponding value in the number. Let us consider the number 64,19,85,062
and write place-value of each digit in the following chart.

We read the above number as thirty-four crore, nineteen lakh,
seventy-five thousand, fifty-two.
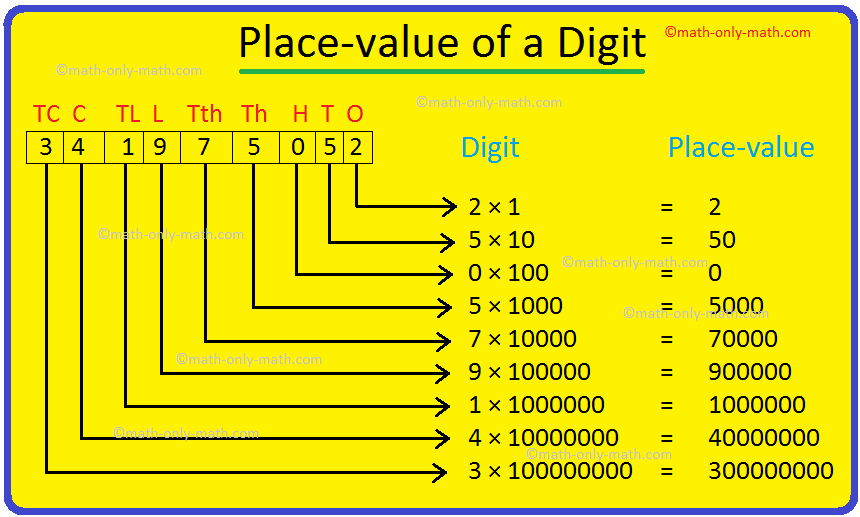
The place-value of a digit in a number depends upon the place it occupies in the place-value chart.
Place-Value of a Digit = Face-Value × Value of the Place it Occupies in the Place-Value Chart.

Note: The
place value of a particular digit in a given number depends on its placing in
the number.
Solved Examples Place-value of a Digit in a Number:
1. Consider the number 9,24,658
Let us arrange the digits of this in the place-value chart :

From the above place-value chart, we have,
8 is at ones place,
so its place-value is 8 ones = 8 × 1 = 8.
5 is at tens place,
so its place-value is 5 tens = 5 × 10 = 50.
6 is at hundreds place,
so its place-value is 6 hundreds =6 × 100 = 600.
4 is at thousands place,
so its place-value is 4 thousands = 4 × 1,000 = 4000.
2 is at ten thousands place,
so its place-value is 2 ten thousands =2 × 10,000 = 20,000.
9 is at lakhs place,
so its place-value is 9 lakhs = 9 × 1,00,000 = 9,00,000.
2. Write the place-value of 3 in each of the following numbers:
(i) 23,584
(ii) 3,70,964
(iii) 9,82,934
Solution: Arrange the digits of the numbers in the place-value chart.
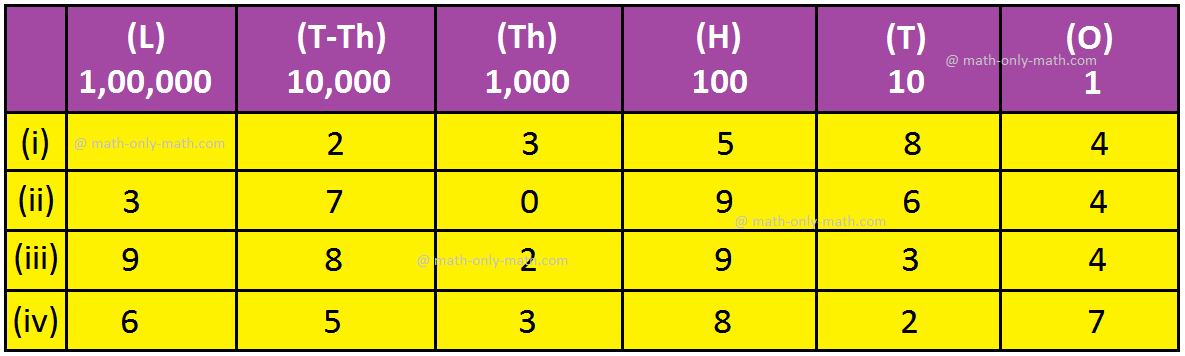
(a) Place-value of 3 in 23,584 = 3 × 1,000 = 3,000.
(b) Place-value of 3 in 3,70,964 = 3 ×1,00,000 = 3,00,0000.
(c) Place-value of 3 in 9,82,934 = 3 × 10 = 30.
(d) Place-value of 3 in 6,53,827 = 3 × 1,000 = 3,000
REMEMBER
The place-value of 0 is always 0, whatever place it occupies in the place-value chart.
3. Write the place-value of 5 in the given numbers:
(i) 50,21,38,761
(ii) 82,05,36,401
(iii) 79,46,15,380
Solution:
Let us arrange the digits in the place-value chart
(i)

Place value of 5 in the number is
5 × 10,00,00,000 = 50,00,00,000. It is read as fifty crore.
(ii)

Place value of 5 in the number is
5 × 1,00,000 = 5,00,000. It is read as five lakh.
(iii)

Place value of 5 in the number is
5 × 1,000 = 5,000. It is read as five thousand.
4. Write the place value of underlined digits in the given blank.
(i) 5,103
(ii) 7,00,496
(iii) 8,15,924
(iv) 2,18,951
Solution:
(i) 5,103
3 being at one’s or unit’s place
The place value of 3 in the number 5,103 is 3.
(ii) 7,00,496
7 being at Lakhs-place
The place value of 7 in the number 7,00,496 is 7,00,000.
(iii) 8,15,924
2 being at Tens-place
The place value of 2 in the number 8,15,924 is 20.
(iv) 2,18,951
2 being at Lakhs-place
The place value of 2 in the number 2,18,951 is 2,00,000.
5. Circle the following.
(i) Digit at lakhs place – 17,45,015
(ii) Digit with face value of 9 – 49,00,781
(iii) Digit at ten crores place – 92,15,55,470
(iv) Digit at ten thousands place – 75,19,778
(v) Digit at tens place – 92,15,55,470
Solution:
(i) 7
(ii) 9
(iii) 9
(iv) 1
(v) 7
6. Find the
place value of 9 in the given numbers.
(i)
6,96,242
(ii)
3,29,162
(iii) 4,52,921
We first
arrange the digits of the given number in the place value chart.
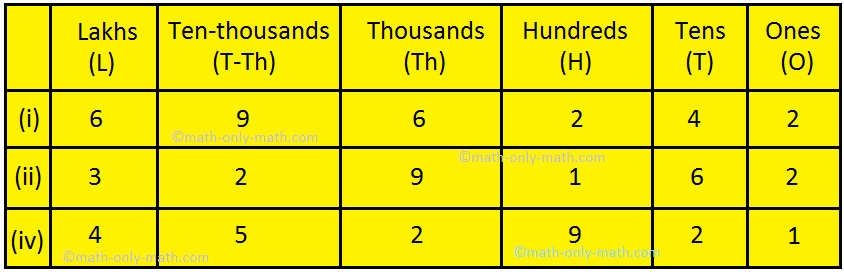
(i) Place value of 9 in the number 6,96,242 is
9 × 10,000 = 90,000
(ii) Place value of 9 in the number 3,29,162 is
9 × 1,000 = 9,000
(iii) Place value of 9 in the number 4,52,921 is
9 × 100 = 900
7. Write the place value of the digit underlined in each
number.
(i) 67843
(ii) 765432
(iii) 865409
(iv) 736524
(v) 800026
Answer:
7. (i) 7000
(ii) 700000
(iii) 5000
(iv) 30000
(v) 20
8. Rewrite using the Indian place-value chart and write the
number name.
(i) 364,875
(ii) 42, 760, 542
(iii) 6,521,324
Answer:
8. (i) 3,64,875; Three lakh sixty-four thousand eight hundred seventy-five.
(ii) 4,27,60,542; Four crore twenty-seven lakh sixty thousand five hundred forty-two
(iii) 65,21,324; Sixty-five lakh twenty-one thousand three hundred twenty-four.
9. Rewrite using the International place-value chart and
write the number name.
(i) 7,24,60,542
(ii) 21,56,324
(iii) 2,83,964
Answer:
9. (i) 72,460,542; Seventy-two million four hundred sixty thousand five hundred and forty-two.
(ii) 2,156,324; Two million one hundred fifty-six thousand three hundred and twenty-four.
(iii) 283,964; Two hundred eighty-three thousand nine hundred and sixty-four.
10. In 2798435, if the hundreds digit is increased by 3, then the
difference between the place values of 7s is
(i) 597300
(ii) 699300
(iii) 569200
(iv) 4995300
Solution:
The given number is 2798435
Hundreds digit is increased by 3
Now the number is 2798735
difference between the place values of 7s = 700000 – 700
= 699300
Correct option is (ii) 699300
11. The difference in the place values of 6’s between the
greatest and smallest numbers formed using the digits 6, 0, 4, 9 is
(i) 4069
(ii) 6540
(iii) 540
(iv) 9640
Solution:
The greatest number formed using the digits 6, 0, 4, 9 is 9640
Place value of 6 in 9640 = 600
The smallest number formed using the digits 6, 0, 4, 9 is 4069
Place value of 6 in 4069 = 60
The difference in the place values of 6’s between the greatest and smallest numbers = 600 – 60 = 540
Correct answer is (iii) 540
Face Value:
Consider the number 3,92,687
It has six digits 3,9,2,6,8 and 7.
We say that in 3,92,687, the face value of 3 is 3, 9 is 9, 2 is 2, 6 is 6, 8 is 8 and 7 is 7.
The face-value of a digit in a number is value of the digit itself regardless of the position of the digit.
Examples:
1. Find the face-value of:
(i) 2 in 3, 46, 294
(ii) 5 in 35, 192
(iii) 8 in 2,62,498
(iv) 6 in 61,490
Solution:
(i) Face-value of 2 in 3,46,294 is 2.
(ii) Face-value of 5 in 35, 192 is 5.
(iii) Face-value of 8 in 2,62,498 is 8.
(iv) Face-value of 6 in 61,490 is 6.
2. Write the face value of red underlined digits in the given blank.
(i) 587
(ii) 604
(iii) 258
(iv) 769
(v) 357
(vi) 832
(vii) 412
(viii) 124
(ix) 329
Solution:
(i) 587 – Face value of 8 is 8
(ii) 604 – Face value of 6 is 6
(iii) 258 – Face value of 5 is 5
(iv) 769 – Face value of 9 is 9
(v) 357 – Face value of 5 is 5
(vi) 832 -Face value of 2 is 2
(vii) 412 – Face value of 4 is 4
(viii) 124 – Face value of 2 is 2
(ix) 329 – Face value of 9 is 9
Activity for understanding place values of digits in 5-and 6-digit numbers using paper strips.
Required Materials: Paper strips of dimensions 20 cm × 5 cm (approx.)
Instructions:
Step I: Take a paper strip and fold it into 6 equal parts as shown.
Step II: Write 3,00,000 in the first box from left of the strip.
Step IV: In the next box write 50,000.
Step V: Similarly, in the next boxes, write 8000, 400, 30 and 7 respectively.
Step V: Now, carefully fold the strip as shown below.
In this way, the folded strip represents the number 358437
Step VI: If we unfold it, it represents the place value of each digit.
In the same way, we can form other numbers and get the place value of each digits.
Solved Examples on Place Value and Face Value:
1. What is the difference between the place value and face value of the
digit 5 in 8795648?
Solution:
Place value of the digit 5 in 8795648 is 5000
Face value of the digit 5 in 8795648 is 5
Therefore, the difference between the place value and face value of the digit 5 in 8795648 = 5000 – 5 = 4995
2. What is the product of the place values of two 4’s in 843940?
Solution:
The product of the place values of two 4’s in 843940 = 40000 × 40
= 1600000
Worksheet on Place Value and Face Value:
1. Fill in the blanks as shown.
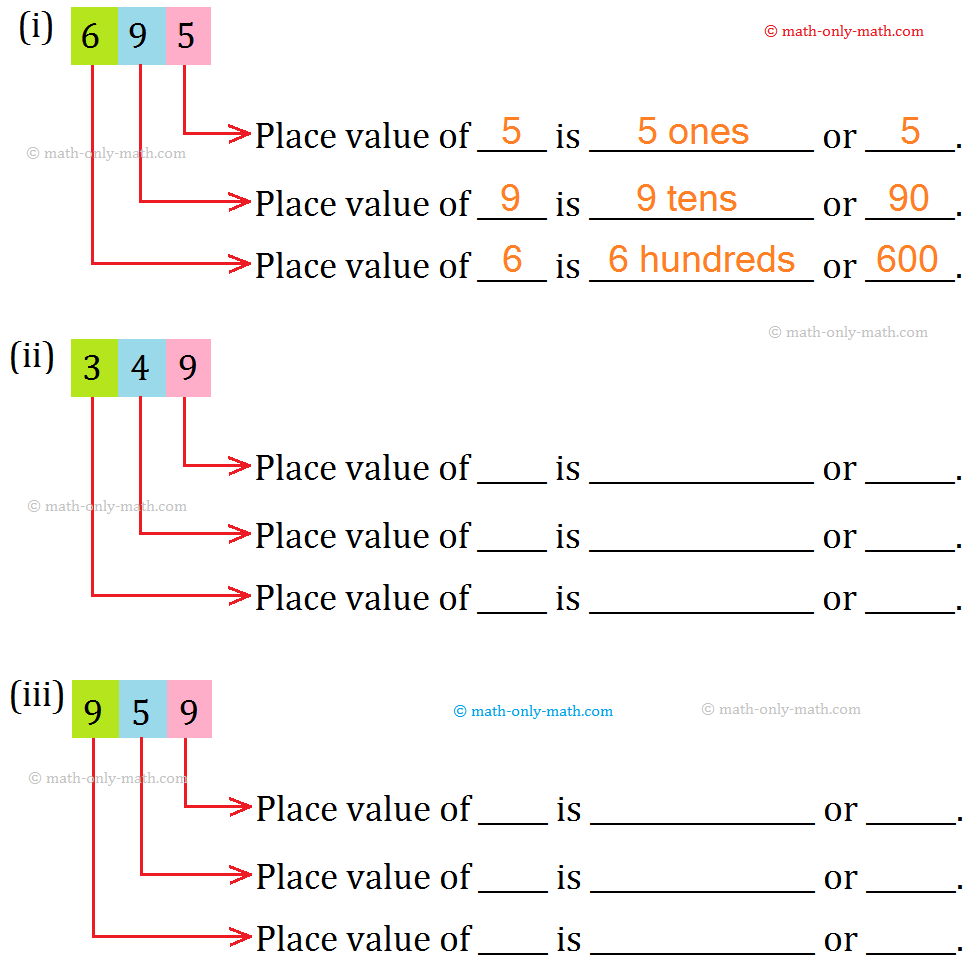
Answer:
1. (ii) Place value of 9 is 9 ones or 9.
Place value of 4 is 4 tens or 40.
Place value of 3 is 3 hundreds or 300.
(iii) Place value of 9 is 9 ones or 9.
Place value of 5 is 5 tens or 50.
Place value of 9 is 9 hundreds or 900.
Math Only Math is based
on the premise that children do not make a distinction between play and
work and learn best when learning becomes play and play becomes
learning.
However, suggestions for further improvement, from all quarters would be greatly appreciated.
Related Concept
4th Grade Math Activities
From Place Value and Face Value to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
